Kaip „SciPy“ yra atviras šaltinis, joje yra labai aktyvi ir gyvybinga kūrėjų bendruomenė, dėl kurios yra labai daug modulių, skirtų daugeliui mokslinių programų ir skaičiavimų, kuriuos galima gauti naudojant „SciPy“. Kai kurios sudėtingos matematinės operacijos, kurias galima atlikti naudojant „SciPy“, yra šios:
- Interpoliacija
- Integracija
- Optimizavimas
- Vaizdo apdorojimas
- Statistika
- Specialieji funkcijos skaičiavimai ir kt.
„SciPy“ galima palyginti su daugeliu komandinių ir standartinių bibliotekų, tokių kaip GSL biblioteka, skirta „C ++“ ir „Matlab“. Kadangi „SciPy“ yra sukurtas ant „NumPy“ paketo, šiuos du paketus taip pat galima visiškai integruoti. Jei sugalvojate apie matematinę operaciją, kurią reikia atlikti, būtinai patikrinkite „SciPy“ biblioteką, prieš pradėdami savarankiškai įdiegti tą modulį, nes daugeliu atvejų „SciPy“ jau turi visas jūsų atliktas operacijas.
Įdiekite „SciPy“ biblioteką
Įdiekime „SciPy“ biblioteką prieš pereidami prie tikrųjų pavyzdžių ir koncepcijų. Šį paketą galite įdiegti dviem būdais. Pirmasis apima „Python“ paketų tvarkyklės „pip“ naudojimą:
pip įdiegti scipyAntrasis būdas susijęs su „Anaconda“, paketą galime įdiegti kaip:
conda install -c anaconda scipyĮdiegę biblioteką, galime ją importuoti kaip:
importuoti scipyGaliausiai, kadangi naudosime ir „NumPy“ (rekomenduojama visoms „NumPy“ operacijoms naudoti „NumPy“, o ne pereiti prie „SciPy“ paketo):
importuoti numerįGali būti, kad kai kuriais atvejais mes taip pat norėsime suskaičiuoti savo rezultatus, kuriems naudosime „Matplotlib“ biblioteką. Atlikite šį tos bibliotekos importavimą:
importuoti matplotlibVisiems šios pamokos pavyzdžiams naudosiu „Anaconda“ valdytoją. Paleisiu „Jupyter“ nešiojamąjį kompiuterį:

Dabar, kai esame pasirengę su visais importo teiginiais parašyti kodą, pradėkime nerti į „SciPy“ paketą su keletu praktinių pavyzdžių.
Darbas su daugianario lygtimis
Pradėsime nuo paprastų daugianario lygčių. Yra du būdai, kaip mes galime integruoti daugianario funkcijas į savo programą. Mes galime pasinaudoti poly1d klasė, kuri naudoja koeficientus arba daugianario šaknis polinomui inicijuoti. Pažvelkime į pavyzdį:
iš numpy importo poly1dfirst_polynomial = poly1d ([3, 4, 7])
spausdinti (pirmasis_polinomas)
Vykdydami šį pavyzdį, pamatysime šį išvestį:

Aišku, kad polinomas lygties atvaizdavimas spausdinamas kaip išvestis, kad rezultatą būtų gana lengva suprasti. Mes taip pat galime atlikti įvairias operacijas su šiuo polinomu, pavyzdžiui, kvadratuoti, rasti jo darinį ar net išspręsti x reikšmę. Pabandykime atlikti visa tai kitame pavyzdyje:
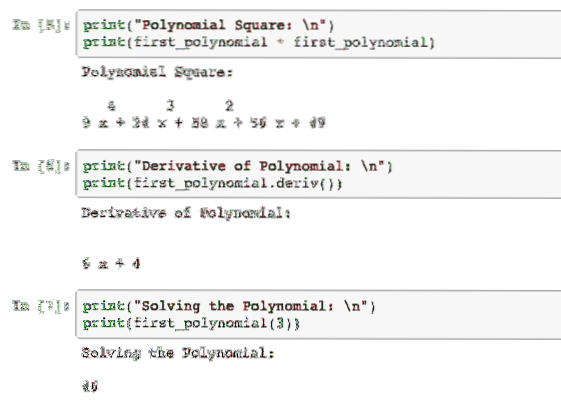
spausdinti ("Polinomo kvadratas: \ n")spausdinti (first_polynomial * first_polynomial)
spausdinti ("Polinomo darinys: \ n")
spausdinti (pirmasis_polinomas.darinys ()
spausdinti ("Polinomo sprendimas: \ n")
spausdinti (pirmasis_polinomas (3))
Vykdydami šį pavyzdį, pamatysime šį išvestį:
Kai galvojau, kad tai viskas, ką galime padaryti su „SciPy“, prisiminiau, kad galime integruoti ir polinomą. Paleiskime paskutinį pavyzdį su polinomais:
spausdinti ("Polinomo integravimas: \ n")spausdinti (pirmasis_polinomas.sveikas (1))
Sveikasis skaičius, kurį praleidome, nurodo paketui, kiek kartų reikia integruoti daugianarį:
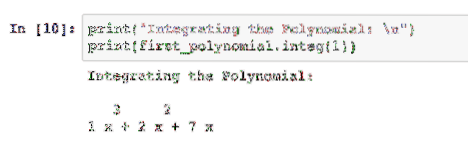
Mes galime tiesiog perduoti kitą sveiką skaičių, kuris paketui nurodo, kiek kartų reikia integruoti šį polinomą.
Tiesinių lygčių sprendimas
Net įmanoma išspręsti linijines lygtis su „SciPy“ ir rasti jų šaknis, jei tokių yra. Norėdami išspręsti tiesines lygtis, lygčių rinkinį vaizduojame kaip „NumPy“ masyvus, o jų sprendimą - kaip atskirus „NumPy“ masyvus. Vizualizuokime tai su pavyzdžiu, kai darome tą patį ir naudojamės linalg paketą, kad surastumėte lygčių šaknis, pateikiame lygtis, kurias mes išspręsime:
1x + 5y = 63x + 7y = 9
Išspręskime aukščiau pateiktas lygtis:
nuo scipy importo linalglygtis = np.masyvas ([[1, 5], [3, 7]])
tirpalas = np.masyvas ([[6], [9]])
šaknys = linalg.išspręsti (lygtis, sprendimas)
spausdinti ("Rado šaknis:")
spauda (šaknys)
spausdinti ("\ n taškų sandauga turėtų būti lygi nuliui, jei teisingi sprendimai:")
spausdinti (lygtis.taškas (šaknys) - tirpalas)
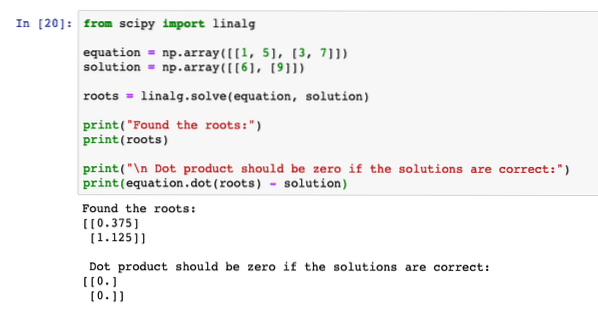
Vykdydami pirmiau nurodytą programą pamatysime, kad taško sandaugos lygtis duoda nulinį rezultatą, o tai reiškia, kad šaknys, kurias rado programa, buvo teisingos:
Furjė transformacijos su SciPy
„Fourier“ transformacijos padeda mums išreikšti funkciją kaip atskirus komponentus, sudarančius tą funkciją, ir nurodo būdą, kaip galime tuos komponentus rekombinuoti, kad atgautume pradinę funkciją.
Pažvelkime į paprastą Furjė transformacijų pavyzdį, kai mes suskaičiuojame dviejų kosinusų sumą naudodami „Matplotlib“ biblioteką:
nuo scipy.fftpack importuoti fft# Mėginių taškų skaičius
N = 500
# pavyzdžio tarpai
T = 1.0/800.0
x = np.linspace (0.0, N * T, N)
y = np.cos (50.0 * 2.0 * np.pi * x) + 0.5 * np.cos (80.0 * 2.0 * np.pi * x)
yf = fft (y)
xf = np.linspace (0.0, 1.0 / (2.0 * T), N // 2)
# matplotlib planavimo tikslams
importuoti matplotlib.pyplotas kaip plt
plt.siužetas (xf, 2.0 / N * np.abs (yf [0: N // 2]))
plt.pavadinimas („Informacija“)
plt.ylabel ('Y ašis')
plt.xlabel ('X ašis')
plt.tinklelis ()
plt.Rodyti()
Čia mes pradėjome konstruoti pavyzdinę erdvę ir kosinuso lygtį, kurią tada transformavome ir nubraižėme. Čia yra pirmiau minėtos programos išvestis:
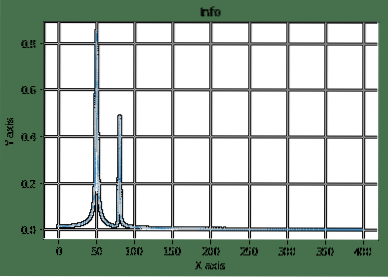
Tai yra vienas iš gerų pavyzdžių, kai matome, kad „SciPy“ yra naudojamas sudėtingoje matematinėje lygtyje, norint lengvai vizualizuoti dalykus.
Vektoriai ir matrica su „SciPy“
Dabar, kai žinome daugybę dalykų, kuriuos „SciPy“ sugeba, galime būti tikri, kad „SciPy“ taip pat gali dirbti su „Vektoriais“ ir „Matrix“. Matricos yra svarbi tiesinės algebros dalis, nes matricos yra tai, ką mes naudojame ir vektorių atvaizdavimui vaizduoti.
Lygiai taip pat, kaip mes nagrinėjome tiesinių lygčių sprendimą su „SciPy“, vektorius galime pavaizduoti np.masyvas () funkcijos. Pradėkime nuo matricos sukūrimo:
my_matrix = np.matrica (np.atsitiktinis.atsitiktinis ((3, 3)))spausdinti (mano_matrica)
Štai aukščiau esančio fragmento išvestis:

Kai kalbame apie matricas, visada kalbame apie savąsias vertes ir savus vektorius. Kalbant paprastais žodžiais, savieji vektoriai yra vektoriai, kurie, padauginę iš matricos, nekeičia savo krypties, priešingai nei dauguma vektorių. Tai reiškia, kad net kai padauginate savybinius vektorius su matrica, egzistuoja vertė (arba savoji vertė), kuri yra vienas iš daugybos veiksnių. Tai reiškia:
Kirvis = λx.Aukščiau pateiktoje lygtyje A yra matrica, λ yra savoji vertė ir x yra vektorius. Parašykime paprastą kodo fragmentą, kad surastume nurodyto vektoriaus savąsias reikšmes:
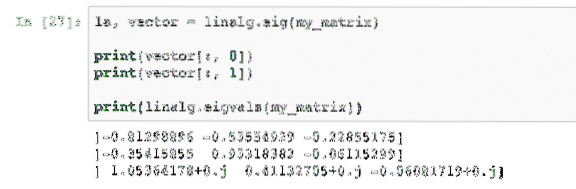
la, vektorius = linalg.eig (mano_matrica)spausdinti (vektorius [:, 0])
spausdinti (vektorius [:, 1])
spausdinti (linalg.eigvalai (mano_matrica))
Vykdydami šį pavyzdį, pamatysime šį išvestį:
Skaičiuojamas matricos determinantas
Kita operacija, kurią atliksime naudodami „SciPy“, yra apskaičiuoti dvimatės matricos determinantą. Matricą, kurią naudojome paskutiniame kodo fragmente, panaudosime čia:
linalg.det (mano_matrica)Vykdydami šį pavyzdį, pamatysime šį išvestį:

Išvada
Šioje pamokoje apžvelgėme daug gerų pavyzdžių, kur „SciPy“ gali mums padėti atlikdami mums sudėtingus matematinius skaičiavimus su lengvai naudojamu API ir paketais.
 Phenquestions
Phenquestions


