„NumPy“ biblioteka leidžia mums atlikti įvairias operacijas, kurias reikia atlikti su duomenų struktūromis, dažnai naudojamomis mašininio mokymosi ir duomenų moksle, pvz., Vektoriais, matricomis ir masyvais. Mes parodysime tik labiausiai paplitusias operacijas su „NumPy“, kurios naudojamos daugelyje „Machine Learning“ vamzdynų. Galiausiai, atkreipkite dėmesį, kad „NumPy“ yra tik būdas atlikti operacijas, todėl matomos matematinės operacijos yra pagrindinis šios pamokos akcentas, o ne pats „NumPy“ paketas. Pradėkime.
Kas yra vektorius?
Pasak „Google“, vektorius yra dydis, turintis kryptį ir dydį, ypač nustatantis vieno taško padėtį erdvėje kito atžvilgiu.
Vektoriai yra labai svarbūs mašininiame mokymesi, nes jie ne tik apibūdina funkcijų dydį, bet ir jų kryptį. „NumPy“ galime sukurti vektorių naudodami šį kodo fragmentą:
importuoti numerį kaip npeilutės_vektorius = np.masyvas ([1,2,3])
spausdinti (row_vector)
Pirmiau pateiktame kodo fragmente sukūrėme eilutės vektorių. Mes taip pat galime sukurti stulpelių vektorių kaip:
importuoti numerį kaip npcol_vector = np.masyvas ([[1], [2], [3]])
spausdinti (col_vector)
Matricos kūrimas
Matricą galima paprasčiausiai suprasti kaip dvimatę masyvą. Matricą galime sukurti naudodami „NumPy“, sudarydami daugialypį masyvą:
matrica = np.masyvas ([[1, 2, 3], [4, 5, 6], [7, 8, 9]])spausdinti (matrica)
Nors matrica yra visiškai panaši į daugiamatę masyvą, matricos duomenų struktūra nerekomenduojama dėl dviejų priežasčių:
- Masyvas yra standartas, kai kalbama apie „NumPy“ paketą
- Dauguma operacijų su „NumPy“ pateikia matricas, o ne matricą
Naudojant retą matricą
Norėčiau priminti, kad reta matrica yra ta, kurioje dauguma elementų yra lygūs nuliui. Dabar dažnas duomenų apdorojimo ir mašininio mokymosi scenarijus yra matricų, kuriose dauguma elementų yra lygūs nuliui, apdorojimas. Pavyzdžiui, apsvarstykite matricą, kurios eilutės apibūdina kiekvieną „YouTube“ vaizdo įrašą, o stulpeliai atspindi kiekvieną registruotą vartotoją. Kiekviena vertė nurodo, ar vartotojas žiūrėjo vaizdo įrašą, ar ne. Žinoma, dauguma šios matricos reikšmių bus lygios nuliui. The pranašumas su reta matrica yra tai, kad jis nesaugo nulinės vertės. Tai taip pat suteikia didžiulį skaičiavimo pranašumą ir saugyklos optimizavimą.
Sukurkime kibirkščių matricą čia:
nuo nenuobodaus importo negaususoriginal_matrica = np.masyvas ([[1, 0, 3], [0, 0, 6], [7, 0, 0]])
reta_matrica = negausi.csr_matrix (original_matrix)
spausdinti (sparse_matrix)
Norėdami suprasti, kaip veikia kodas, apžvelgsime išvestį čia:
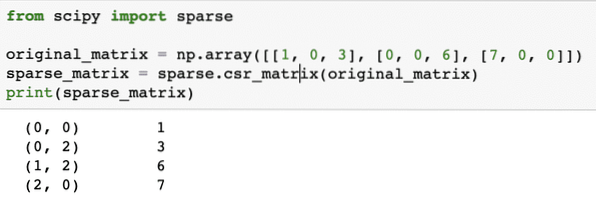
Pirmiau pateiktame kode mes naudojome „NumPy“ funkciją, kad sukurtume Suspausta reta eilė matrica, kurioje nulio elementai vaizduojami naudojant nulinius indeksus. Yra įvairių rūšių retų matricų, tokių kaip:
- Suspausta reta kolona
- Sąrašų sąrašas
- Raktų žodynas
Čia mes nardysime į kitas retas matricas, bet žinome, kad kiekviena jų yra specifinė ir niekas negali būti vadinamas „geriausiu“.
Operacijų taikymas visiems vektoriaus elementams
Tai yra įprastas scenarijus, kai turime taikyti bendrą operaciją keliems vektoriniams elementams. Tai galima padaryti apibrėžiant lambda ir tada vektorizuojant tą patį. Pažiūrėkime keletą to paties kodo fragmentų:
matrica = np.masyvas ([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
mul_5 = lambda x: x * 5
vectorized_mul_5 = np.vektorizuoti (mul_5)
vectorized_mul_5 (matrica)
Norėdami suprasti, kaip veikia kodas, apžvelgsime išvestį čia:

Pirmiau pateiktame kodo fragmente mes panaudojome vektorizavimo funkciją, kuri yra „NumPy“ bibliotekos dalis, kad paprastą lambda apibrėžimą paverstume funkcija, galinčia apdoroti kiekvieną vektoriaus elementą. Svarbu pažymėti, kad vektorizavimas yra tik kilpa per elementus ir tai neturi jokios įtakos programos vykdymui. NumPy taip pat leidžia transliacija, o tai reiškia, kad vietoj minėto sudėtingo kodo mes galėjome tiesiog padaryti:
matrica * 5O rezultatas būtų buvęs lygiai toks pats. Pirmiausia norėjau parodyti sudėtingą dalį, kitaip jūs būtumėte praleidę skyrių!
Vidurkis, dispersija ir standartinis nuokrypis
Naudojant „NumPy“, lengva atlikti operacijas, susijusias su aprašomąja vektorių statistika. Vektoriaus vidurkį galima apskaičiuoti taip:
np.vidurkis (matrica)Vektoriaus dispersiją galima apskaičiuoti taip:
np.var (matrica)Standartinį vektoriaus nuokrypį galima apskaičiuoti taip:
np.standartinis (matrica)Aukščiau nurodytų komandų išvestis duotoje matricoje pateikiama čia:

Matricos perkėlimas
Perkėlimas yra labai dažna operacija, apie kurią išgirsite visada, kai jus supa matricos. Perkėlimas yra tik būdas pakeisti matricos stulpelių ir eilučių reikšmes. Atkreipkite dėmesį, kad a vektoriaus negalima perkelti kaip vektorius yra tik reikšmių rinkinys be tų verčių skirstymo į eilutes ir stulpelius. Atkreipkite dėmesį, kad eilutės vektoriaus pavertimas stulpelio vektoriu nėra perkėlimas (remiantis linijinės algebros apibrėžimais, kurie nepatenka į šios pamokos taikymo sritį).
Kol kas ramybę rasime tiesiog permesdami matricą. Labai paprasta pasiekti matricos perkėlimą naudojant „NumPy“:
matrica.TAukščiau nurodytos komandos išvestis duotoje matricoje pateikiama čia:
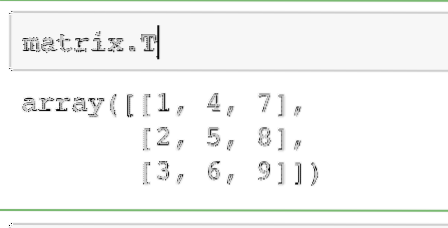
Tą pačią operaciją galima atlikti eilutės vektoriuje, norint konvertuoti jį į stulpelio vektorių.
Matricos išlyginimas
Matricą galime paversti vienos dimensijos masyvu, jei norime jos elementus apdoroti linijiniu būdu. Tai galima padaryti naudojant šį kodo fragmentą:
matrica.išlyginti ()Minėtos komandos išvestis duotoje matricoje pateikiama čia:

Atkreipkite dėmesį, kad išlyginta matrica yra vienos dimensijos masyvas, tiesiog linijinis.
Atskirų verčių ir savitųjų vektorių skaičiavimas
Savieji vektoriai labai dažnai naudojami mašininio mokymosi paketuose. Taigi, kai linijinės transformacijos funkcija pateikiama kaip matrica, tada X, savieji vektoriai yra vektoriai, kurie keičiasi tik vektoriaus mastu, bet ne jo kryptimi. Galime pasakyti, kad:
Xv = γvČia X yra kvadratinė matrica, o γ yra savosios vertės. Be to, v yra savieji vektoriai. Naudojant „NumPy“, lengva apskaičiuoti savąsias reikšmes ir vektorius. Štai kodo fragmentas, kuriame mes demonstruojame tą patį:
evalues, evectors = np.linalg.eig (matrica)Aukščiau nurodytos komandos išvestis duotoje matricoje pateikiama čia:
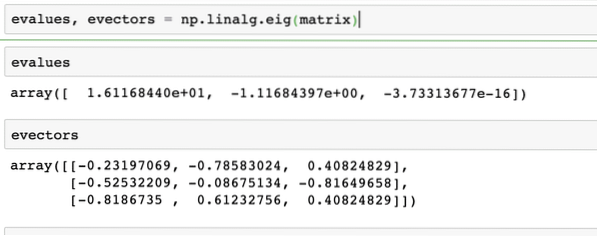
Taškiniai vektorių gaminiai
Taškiniai vektorių produktai yra būdas padauginti 2 vektorius. Tai jums pasakoja apie kiek vektorių yra ta pačia kryptimi, priešingai nei kryžminis produktas, kuris jums sako priešingai, kiek mažai vektorių yra ta pačia kryptimi (vadinama stačiakampiu). Dviejų vektorių taškų sandaugą galime apskaičiuoti taip, kaip nurodyta kodo fragmente:
a = np.masyvas ([3, 5, 6])b = np.masyvas ([23, 15, 1])
np.taškas (a, b)
Aukščiau nurodytos komandos išvestis duotuose masyvuose pateikiama čia:

Matricų susiejimas, atimimas ir dauginimas
Kelių matricų pridėjimas ir atėmimas yra gana paprastas matricų veiksmas. Tai galima padaryti dviem būdais. Pažvelkime į kodo fragmentą, kad atliktume šias operacijas. Kad tai būtų paprasta, tą pačią matricą naudosime du kartus:
np.pridėti (matrica, matrica)Tada dvi matricas galima atimti kaip:
np.atimti (matrica, matrica)Aukščiau nurodytos komandos išvestis duotoje matricoje pateikiama čia:
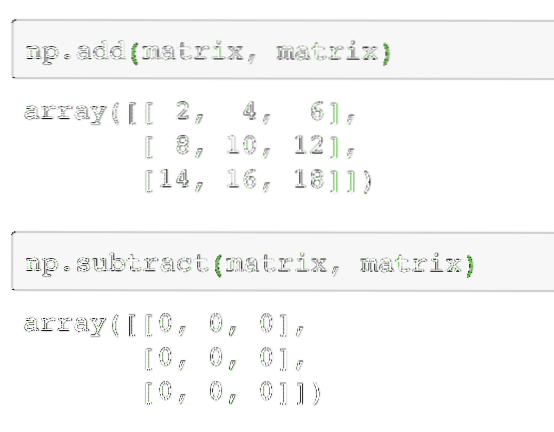
Kaip ir reikėjo tikėtis, kiekvienas iš matricos elementų pridedamas / atimamas su atitinkamu elementu. Matricos padauginimas yra panašus į taškinio produkto paiešką, kaip tai darėme anksčiau:
np.taškas (matrica, matrica)Aukščiau pateiktas kodas suras tikrąją dviejų matricų daugybos vertę, pateiktą kaip:
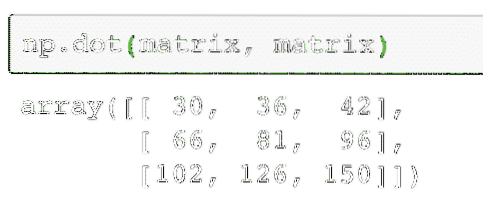
Aukščiau nurodytos komandos išvestis duotoje matricoje pateikiama čia:

Išvada
Šioje pamokoje patyrėme daug matematinių operacijų, susijusių su vektoriais, matricomis ir masyvais, kurie dažniausiai naudojami Duomenų apdorojimas, aprašomoji statistika ir duomenų mokslas. Tai buvo greita pamoka, apėmusi tik pačius dažniausiai pasitaikančius ir svarbiausius įvairių sąvokų skyrius, tačiau šios operacijos turėtų labai gerai suprasti, ką visas operacijas galima atlikti tvarkant šias duomenų struktūras.
Prašau laisvai pasidalinti savo atsiliepimais apie pamoką „Twitter“ su @linuxhint ir @sbmaggarwal (tai aš!).
 Phenquestions
Phenquestions


